Pullback along monotone(1)
A pullback along a monotone map \(P \xrightarrow{f} Q\)
We take the preimage of \(f\), but not for a single element of \(Q\) but rather an upper set of \(Q\).
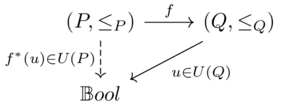
Noting that upper sets are monotone maps to Bool, it follows that the result of a pullback is an upper set in \(P\) follows from the fact that composition preserves monotonicity.
Therefore the type of the pullback is \(U(Q) \xrightarrow{f^*} U(P)\)
